Teorema de Pitágoras
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos. Es la proposición más conocida, entre otras, de las que tienen nombre propio de la matemática
Si un triángulo rectángulo tiene catetos de longitudes y , y la medida de la hipotenusa es , se formula que:
De la ecuación (1) se deducen fácilmente tres corolarios de verificación algebraica y aplicación práctica:
Pensamiento DE Pitágoras
El Teorema de Pitágoras puede haberse conocido mucho antes del nacimiento de Pitágoras, pero fue comprobado en el siglo VI a.C. por el matemático Pitágoras.
Respecto de los babilonios hay esta nota:
Desde el punto de vista matemático, las novedades más importantes que registran los textos babilónicos se refieren a la solución algebraica de ecuaciones lineales y cuadráticas, y el conocimiento del llamado "teorema de Pitágoras" y de sus consecuencias numéricas.
Desde el punto de vista matemático, las novedades más importantes que registran los textos babilónicos se refieren a la solución algebraica de ecuaciones lineales y cuadráticas, y el conocimiento del llamado "teorema de Pitágoras" y de sus consecuencias numéricas.
El teorema de Pitágoras tiene este nombre porque su demostración, sobre todo, es esfuerzo de la mística escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se corresponden con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros. Sin
embargo, no ha perdurado ningún documento que exponga teóricamente su relación.3 La pirámide de Kefrén, datada en el siglo XXV I a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
embargo, no ha perdurado ningún documento que exponga teóricamente su relación.3 La pirámide de Kefrén, datada en el siglo XXV I a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
| Vértices | |||
| Lados (como segmento) | |||
| Lados (como longitud) | |||
| Ángulos |
Demostraciones:
El teorema de Pitágoras es de los que cuenta con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Una de las causas de esto es que en la Edad Media se exigía una nueva demostración del teorema para alcanzar el grado de "Magíster matheseos".
Algunos autores proponen hasta más de mil demostraciones. Otros autores, como el matemático estadounidense E. S. Loomis, catalogó 367 pruebas diferentes en su libro de 1927 The Pythogorean Proposition.
En ese mismo libro, Loomis clasificaría las demostraciones en cuatro grandes grupos: las algebraicas, donde se relacionan los lados y segmentos del triángulo; geométricas, en las que se realizan comparaciones de áreas; dinámicas a través de las propiedades de fuerza, masa; y las cuaterniónicas, mediante el uso de vectores.
Problema 1
- Los lados son. ...
- Llamamos a los lados a y b y a la hipotenusa h. ...
- Llamamos a los catetos a y b y a la hipotenusa h (no importa el nombre que le demos a cada cateto). ...
- Para poder calcular la altura del triángulo, a, tenemos que dividirlo en dos triángulos rectángulos (para poder aplicar el teorema de Pitágoras)
Problemas Resueltos del Teorema de Pitágoras:
- Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm.
Los lados son
Aplicando el teorema de Pitágoras,
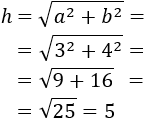
Por tanto, la hipotenusa mide 5 cm.
2. Si la hipotenusa de un triángulo rectángulo mide 2cm y uno de sus lados mide 1 cm, ¿cuánto mide el otro lado?
Aplicando el teorema de Pitágoras,
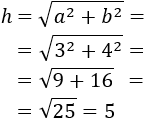
Por tanto, la hipotenusa mide 5 cm.
2. Si la hipotenusa de un triángulo rectángulo mide 2cm y uno de sus lados mide 1 cm, ¿cuánto mide el otro lado?
Llamamos a los lados a y b y a la hipotenusa h. Sabemos que
Por Pitágoras, sabemos que
Sustituyendo los valores conocidos tenemos que

Ahora despejamos b en la ecuación
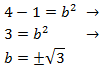
Hemos escrito los signos positivo y negativo porque es lo que, en teoría, debemos hacer. Pero como b representa la longitud de un cateto, no puede ser un número negativo.
Por tanto, el cateto mide
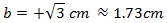
Podemos dejar la raíz cuadrada o aproximarla.
Por Pitágoras, sabemos que
Sustituyendo los valores conocidos tenemos que

Ahora despejamos b en la ecuación
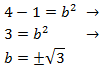
Hemos escrito los signos positivo y negativo porque es lo que, en teoría, debemos hacer. Pero como b representa la longitud de un cateto, no puede ser un número negativo.
Por tanto, el cateto mide
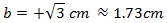
Podemos dejar la raíz cuadrada o aproximarla.
3 Calcular la hipotenusa del triángulo rectángulo cuyos lados miden 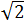 y
y 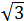 .
.
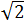 y
y 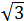 .
.
Llamamos a los catetos a y b y a la hipotenusa h (no importa el nombre que le demos a cada cateto).
Sabemos que
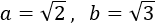
Por el teorema de Pitágoras, sabemos que
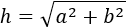
Sustituimos en la ecuación los valores conocidos (a y b), obteniendo:
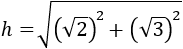
Recordamos que el cuadrado de una raíz cuadrada es su radicando (lo de dentro de la raíz), por tanto,
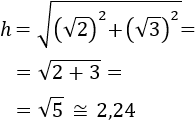
Por tanto, la hipotenusa mide aproximadamente 2.24. No indicamos la unidad de medida (mm, cm, dm, m…) ya que no se indica en el enunciado.
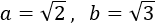
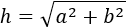
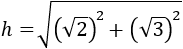
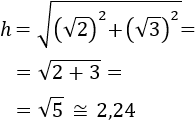





















No hay comentarios.:
Publicar un comentario